Spart eine Kondensatanstauregelung wirklich Energie?

Eine detaillierte Betrachtung.

Dampfbeheizte Wärmeübertragerstationen für Wasser kommen in vielen Industriezweigen zum Einsatz. Hoher Wärmeinhalt, hoher Wärmeübergang und eine gute Regelbarkeit sprechen für das Heizmedium Dampf. Durch die Abgabe von Wärme an ein aufzuheizendes Medium kondensiert der Dampf wieder zu Kondensat genanntem Wasser. Dieses wird zum Kesselhaus zurückgeführt und kommt erneut im Dampfkessel zum Einsatz, denn Kondensat ist bereits chemisch neutral und verfügt über eine Restenergie.

Bei der Regelung von Wärmeübertragern unterscheidet man zwischen einer dampfseitigen Regelung und einer Kondensatanstauregelung mit unterschiedlichen Eigenschaften. Eine der Kondensatanstauregelung zugesprochenen Eigenschaften ist eine Dampfersparnis von ca. 20% im Vergleich zur dampfseitigen Regelung. Das klingt verlockend, daher möchte dieser Beitrag diese mögliche Einsparung objektiv und rechnerisch untersuchen.

Die Wärmeübertragung

Gleichungen der Wärmeübertragung

Damit eine Wärmeübertragung stabil erfolgen kann, müssen 3 Gleichungen erfüllt sein:

Wärmebedarf des Produktes: QP = mP * cP * (T2-T1)

QP: benötigte Wärmemenge des Produkts zum Aufheizen des Massenstroms [kJ/h]
mP: Massenstrom Produkt [kg/h]
cP: spezifische Wärmekapazität des zu beheizenden Mediums [kJ / kg K]
T1: Eintrittstemperatur des Produkts [°C], T2: Austrittstemperatur des Produkts [°C]

Übertragene Wärmemenge: QWÜT = k * A * LMTD

QWÜT: übertragene Wärmemenge zum Aufheizen des Produkts [kJ/h]
k: Wärmedurchgangskoeffizient [W / m2 K]
A: Wärmeübertragerfläche [m2]
LMTD: mittlere logarithmische Temperaturdifferenz [K]

Wärmeinhalt des Heizdampfes: QS = mS * hS

QS: gelieferte Wärmemenge des Dampfes zum Aufheizen des Produkts [kJ/h]
mS: Massenstrom Dampf [kg/h]
hS: Enthalpie des Dampfes [kJ/kg]

Merkmale der Regelungsarten

Dampfseitige Regelung

  • Schnelles Ansprechen der Regelung
    -> Durch Änderung Öffnung Regelventil
  • QWÜT = k * A * LMTD
  • Freie Ablauf Kondensat – keine Korrosion
  • Evtl. Kondensatrückstau bei Gegendruck Pump-Kondensatableiter empfohlen
  • Entstehung von Nachdampf in Kondensatleitung

Kondensatanstauregelung

  • Träges Ansprechen der Regelung, da weiteres Anstauen oder Ablassen von Kondensat erforderlich ist => kann bei Lastwechseln zu Temperaturschwankungen führen
  • QWÜT = k * A * LMTD
  • Evtl. Korrosion durch angestautes Kondensat
  • Kein Kondensatrückstau durch konstanten Dampfdruck
  • Unterkühlung des Kondensats, daher meist kein Nachdampf
  • Durchschlagen von Dampf möglich
  • Kleinere Armaturen, aber verstärkter Wärmeübertrager nötig, evtl. preisgünstiger

 

 

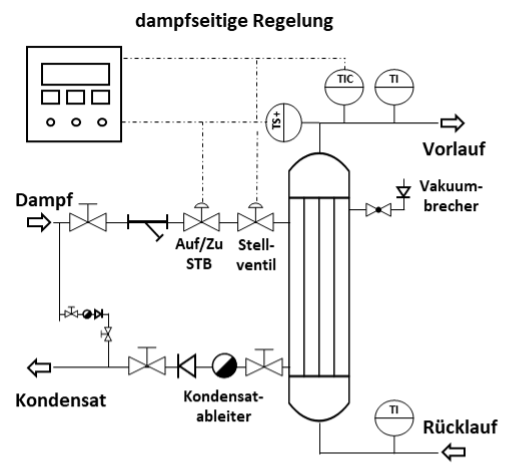
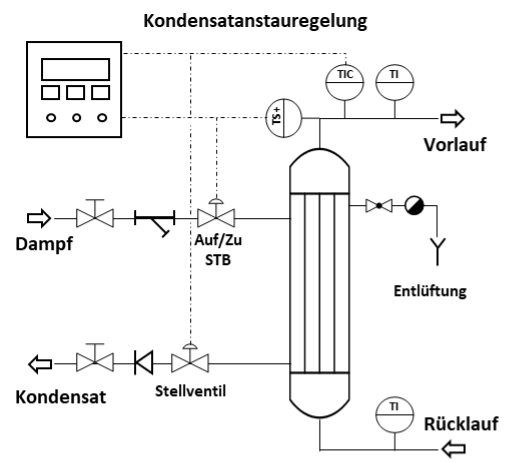
Berechnung der benötigten Wärmemengen im Dampfsystem

Für einen objektiven Vergleich ist es erforderlich, die benötigten Wärmemengen rechnerisch zu ermitteln. Dies kann anschaulich anhand des Beispiels einer typischen Heizungsanwendung erfolgen:

 

Betrachtung des Systems Wärmeübertrager

Anwendung: Erwärmung von Wasser für eine Gebäudeheizung

Erwärmung von 10 m3/h Wasser, von 50°C auf 70°C

Zur Verfügung stehender Dampfdruck: 3 bar ü

 

Wärmebedarf des Produktes

QP = mP * cP * (T2-T1) = 10.000 kg/h * 4,18 kJ / kg K * (70°C – 50°C) = 836.000 kJ/h = 232,2 kW

 

Benötigte Dampfmenge

3 bar ü (143,73°C): Verdampfungswärme r = 2.132,97 kJ/ kg

mS = QS / hS = 836.000 kJ/h / 2.133 kJ/ kg = 391,9 kg/h Dampf bei 3 bar ü

 

Gegenüberstellung der benötigten Dampfmenge im System Wärmeübertrager

Dampfseitige Regelung

  • Nachdampf zu 0 bar ü (offenes Rückführsystem: 8,3 % <=> 32,3 kg/h
  • bei 100°C <=> 86.420
  • mit 2675,63 kJ/kg Gesamtenthalpie kJ/h
 Kondensatanstauregelung

  • Unterkühlung des Kondensats und Nutzung fühlbarer Wärme
  • Annahme: sehr gute Unterkühlung auf 60°C (Unterkühlung um 83 K!)
  • Fühlbare Wärme 3 bar ü: 605,24 kJ/kg
  • Fühlbare Wärme 60°C: 251,15 kJ/kg
  • Differenz: 351,09 kJ/kg
  • => neue verfügbare Wärmemenge: (2.132,97 + 351,09) kJ/kg = 2.484,06 kJ/kg
– benötigte Dampfmenge 391,9 kg/h Dampf bei 3 bar ü – benötigte Dampfmenge 836.000 kJ/h / 2.484,06 kJ/ kg = 336,5 kg/h

Reduktion Dampfmenge im WÜT: 14,1 %

 

Gegenüberstellung im System Kondensatleitung

Wir unterstellen ein offenes Kondensatrückführsystem mit atmosphärischem Druck. Ein geschlossenes Kondensatrückführsystem ist sicherlich energetisch am effizientesten, aber auch in der Ausführung aufwändiger und unterliegt noch anderen Überlegungen.

Dampfseitige Regelung

  • vorhanden bei 100°C:
  • 32,3 kg/h Nachdampf: 86.420 kJ/h
  • 359,6 kg/h Kondensat: 150.669 kJ/h
  • (fühlbare Wärme 418,99 kJ/kg)
 Kondensatanstauregelung

  • vorhanden bei 60°C:
  • 336,5 kg/h Kondensat: 84.512 kJ/h
  • (fühlbare Wärme 251,15 kJ/kg)

 

Wärmeabstrahlung der Kondensatleitung

Annahmen: Kondensatleitung DN80, 50 mm Isolierung Steinwolle, ca. 100 m Länge, Außentemperatur im Mittel ca. 15°C, 2 m/s Windtemperatur.

Dampfseitige Regelung

  • Medientemperatur 100°C
  • Wärmeverlust: 3.004 W = 10.814,4 kJ/h
 Kondensatanstauregelung

  • Medientemperatur 60°C
  • 1.518 W = 5.464,8 kJ/h
Kondensation von Nachdampf mit 0 bar ü

  • r = 2.256,54 kJ/kg
  • => 10.814,4 kJ/h / 2.256,54 kJ/kg
  • = 4,8 kg /h Nachdampf kondensieren
 Abkühlung von 60°C Kondensat

  • 5.464,8 kJ/h / 336,5 kg/h = 16,24 kJ/kg
  • => (251,15-16,24) kJ/kg = 234,91 kJ/kg
  • => Abkühlen des Kondensats auf 56,1°C

Nach Kondensation bzw. Abkühlung
vorhanden bei 100°C:

  • 27,5 kg/h Nachdampf: 73.577 kJ/h
  • 364,4 kg/h Kondensat: 152.720 kJ/h
  • (fühlbare Wärme 418,99 kJ/kg)
 vorhanden bei 56,1°C:

  • 336,5 kg/h Kondensat: 79.024 kJ/h
  •   (fühlbare Wärme 234,91 kJ/kg)

 

Gegenüberstellung im System Entgaser

Kondensat und Speisewasser muss im Entgaser auf min. 105°C erhitzt werden, um alle nicht-kondensierbaren Gase auszutreiben.

Dampfseitige Regelung

  • 364,4 kg/h Kondensat von 100° auf 105°C
  • fühlbare Wärme 100°C: 418,99 kJ/kg
  • fühlbare Wärme 105°C: 440,21 kJ/kg
 Kondensatanstauregelung

  • 336,5 kg/h Kondensat von 56,1°C auf 105°C
  • fühlbare Wärme 56,1°C: 234,91 kJ/kg
  • fühlbare Wärme 105°C: 440,21 kJ/kg
Benötigte Wärmemenge:

  • 364,4 kg/h * (440,21-418,99) kJ/kg =
  • 7.732,59 kJ/h
 Benötigte Wärmemenge:

  • 336,5 kg/h * (440,21-234,91) kJ/kg =
  • 69.083,45 kJ/h
  • Heizdampf Entgaser = 0,2 bar ü
  • Verdampfungswärme r = 2.242,91 kJ/kg
  • Heizdampf Entgaser = 0,2 bar
  • Verdampfungswärme r = 2.242,91 kJ/kg
Dampfbedarf bei 0,2 bar ü                            

7.732,59 kJ/h / 2.242,91 kJ/kg = 3,4 kg/h

 Dampfbedarf bei 0,2 bar ü

69.083,45 kJ/h / 2.242,91 kJ/kg = 30,8 kg/h

 

Gesamtbilanz

Dampfseitige Regelung

Dampfbedarf:

391,9 kg/h WÜT + 3,4 kg/h Entgaser =

= 395,3 kg/h Dampf – Nachdampf 

27,5 kg/h = 367,8 kg/h

 Kondensatanstauregelung

Dampfbedarf:

336,5 kg/h WÜT + 30,8 kg/h Entgaser =

367,3 kg/h Dampf
Differenz: 0,5 kg/h Dampf (mit Rundungsfehlern gesamte Berechnung)

 

Weitere technische Effekte einer Kondensatanstauregelung

– Bei unterkühltem Kondensat mit niedrigen Temperaturen kann es zu teils starken Wasserschlägen an Punkten kommen, an denen Hochdruckkondensat eingeleitet wird und der entsprechende heiße Nachdampf schlagartig kondensiert.

– Bei niedrigen Kondensattemperaturen kann es in offenen Kondensatrückführsystemen zu Bildung von hochkorrosiver Kohlensäure kommen.

– Bei einer Kondensatanstauregelung kann es zu Dampfdurchschlag kommen, wenn kein Kondensatableiter hinter dem Stellventil installiert ist.

 

Fazit

Diese detaillierte Betrachtung widerlegt rechnerisch, mit einer Kondensatanstauregelung im Vergleich zur dampfseitigen Regelung Energie einsparen zu können. Berücksichtigt man nur losgelöst den Wärmeübertrager, ergibt sich zwar eine gewisse Einsparung, dargelegt anhand eines Anwendungsbeispiels mit einer großzügig ausgelegten Unterkühlung des Kondensats. Bilanziert man hingegen das gesamte Dampf- und Kondensatsystem, muss die vermeintlich eingesparte Dampfmenge dem unterkühlten Kondensat am Entgaser wieder zugeführt werden!

Ein anderes Ergebnis hätte in einem Kreislauf überrascht und den Energieerhaltungssatz außer Kraft gesetzt. Ein möglicher Verlust einer dampfseitigen Regelung kann in Form von Nachdampf erfolgen, dessen Rückgewinnung aber heute Standard ist.

Die Kondensatanstauregelung hat durchaus ihre Berechtigung bei sehr gleichmäßigen Prozessen, wie etwa in der Fernwärme.

Eine dampfseitige Regelung ist aufgrund ihrer schnellen Regelung vielseitig auch in Prozessen einsetzbar, und Effekte wie Wasserschläge oder erhöhte Korrosion können minimiert werden.